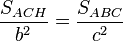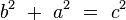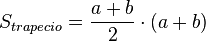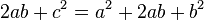OPERACIONES ALGEBRAICAS BÁSICAS.
En este apartado vamos a realizar las operaciones algebraicas básicas que nos
permiten utilizar DERIVE como herramienta de cálculo. Todas estas operaciones las
realizaremos sobre una ventana de álgebra, por lo que los comandos que vamos a
utilizar están asociados a menús o barras de herramientas de una ventana de álgebra.
Nos situamos por tanto sobre una ventana de álgebra.
2.1 SIMPLIFICAR EXPRESIONES.
Para utilizar DERIVE como una calculadora, basta iluminar la expresión que se
desea simplificar y a continuación aplicar el comando del menú Simplificar-Normal.
Si la expresión no ha sido introducida en la ventana de álgebra, existe la
posibilidad de simplificarla directamente desde la ventana de edición. También se
utiliza el botón de herramientas
Así por ejemplo, si introducimos con la expresión “35*(8984-4357)^3” y
aplicamos el botón el comando se obtiene
Con este comando también podemos realizar simplificaciones de operaciones
algebraicas. Por ejemplo, podemos intentar simplificar la expresión
“(x^2-4)/((x-2)(x+3))”. Para ello primero la editamos con y en segundo lugar
aplicamos el comando de simplificar expresión con el botón de herramientas
resultando
También se utiliza este comando para efectuar las operaciones que algunas veces
quedan indicadas como el cálculo de derivadas, integrales, ... más adelante veremos
esta aplicación.
EJERCICIO 13.
Calcular mediante DERIVE los siguientes valores:
a) 500!
b) Ln(45)-4
2.2.TRABAJAR EN MODO APROXIMADO Y MODO EXACTO.
En el apartado b) del ejercicio anterior se puede observar que el resultado
obtenido al simplificar la expresión “ln(45)-4” nos aparece la misma expresión, ¿por
qué? DERIVE siempre trabaja por defecto en MODO EXACTO, por lo que siempre al
simplificar obtenemos como resultado un número exacto. Es una de las características
fundamentales de los programas de cálculo simbólico: la aritmética exacta. Pero si
deseamos calcular expresiones aproximadas en coma flotante, con un cierto número de
Prácticas de Matemáticas I y Matemáticas II con DERIVE 28
decimales podemos aplicar el comando de aproximación que se aplica usando o bien la
secuencia de menú Simplificar-Aproximar o bien utilizando el botón de herramientas
Aproximar . Por ejemplo, si aplicamos este comando a la expresión anterior nos
da
Hemos obtenido en este caso una aproximación con 6 dígitos decimales, que es la
aproximación por defecto que tiene definida DERIVE. Sin embargo podemos
modificarla, indicando el número de dígitos decimales que deseemos. Efectivamente,
si abrimos la ventana de diálogo Modos de Simplificación, con la secuencia de menú
Definir-Modos de operar-Simplificación nos aparece la ventana de diálogo
En el campo PRECISION podemos seleccionar el número de dígitos de
precisiónpara la aproximación.
EJERCICIO 14.
Obtener valores aproximados con 14 dígitos de las siguientes expresiones:
a) el número pi b) el número e c) ln(2) d) e5
2.3.EXPANDIR UNA EXPRESIÓN.
Para expandir o desarrollar una expresión utilizaremos la secuencia de menú
Simplificar-Expandir. Al aplicar esta secuencia sobre cierta expresión previamente
iluminada nos aparece la siguiente ventana de diálogo
Operaciones algebraicas básicas 29
En esta ventana de diálogo podemos seleccionar las variables respecto de las
cuales deseamos expandir y el tipo de expansión: trivial, sin cuadrados, Racional y
Radicales. Normalmente utilizaremos la expansión trivial, iluminando este campo; y
en el campo Variables iluminaremos con el ratón aquellas variables respecto de las
cuales se desea efectuar la expansión (suelen iluminarse todas). Una vez hecho esto
hacemos clic sobre el botón EXPANDIR.
Por ejemplo si deseamos expandir la expresión "(x+y)4
", introducimos primero
esta expresión en la ventana de álgebra con Edición Expresión y a continuación
aplicamos la secuencia de menú Simplificar-Expandir luego aplicamos nuevamente el
botón EXPANDIR resultando
EJERCICIO 15.
Desarrollar o expandir las expresiones
a) (a3
-b)8
b) (2x-y/3)6
c)
1
5 1 4 −
−
x
x
2.4. FACTORIZAR UN NÚMERO.
Obtener la descomposición en factores primos de un número entero es sencilla,
basta con introducir el número como expresión y aplicar sobre esta la secuencia de
menú Simplificar-Factorizar , inmediatamente aparece la siguiente ventana de diálogo
para factorizar un número es suficiente con elegir el campo TRIVIAL, y hacer clic
sobre el botón FACTORIZAR. Por ejemplo, si intentamos calcular la descomposición
en factores primos del número “1470512848896” debemos primero editar la expresión
y aplicar Simplificar-Factorizar elegir el campo TRIVIAL y factorizar, resultando
Prácticas de Matemáticas I y Matemáticas II con DERIVE 30
EJERCICIO 16
Calcular el máximo común divisor de los números 259308 y 7200.
2.5.FACTORIZAR UN POLINOMIO.
DERIVE permite realizar distintos tipos de factorizaciones de polinomios: Todos
ellos se obtienen aplicando la secuencia de menú Simplificar-Factorizar como puede
observarse en la ventana de diálogo en el campo FORMA:
Eligiendo en el campo FORMA el tipo de factorización deseada sobre la expresión
polinómica introducida en la línea de edición.
Para entender como operan cada una de estas opciones vamos a introducir un
polinomio sobre el cual iremos observando el resultado obtenido al aplicar cada uno
de los comandos. Introduzcamos por tanto con el polinomio:
x
8
+2x7
-3x6
-10x5
-8x4
+6x3
+16x2
+8x
a) Si aplicamos la secuencia Simplificar-Factorizar y elegimos en el campo
Forma la opción TRIVIAL, podemos sacar factor común al polinomio si es
que este lo tiene, en nuestro ejemplo obtendríamos
b) Aplicando la secuencia Simplificar-Factorizar, y eligiendo en el campo Forma
la opción LIBRE DE CUADRADOS obtenemos la expresión
Operaciones algebraicas básicas 31
c) Mediante la secuencia Simplificar-Factorizar y eligiendo en el campo Forma
la opción RACIONAL, obtenemos la factorización racional del polinomio
dado
d) La secuencia Simplificar-Factorizar y eligiendo en el campo Forma la opción
RADICAL efectúa una factorización real del mismo
e) Y por último con Simplificar-Factorizar COMPLEJO se realiza una
factorización polinómica utilizando raíces complejas
OBSERVACION: Si se intentan factorizar polinomios de varias variables,
deberemos elegir las variables sobre las cuales se desea efectuar la factorización.
EJERCICIO 17.
Calcular las raíces enteras del polinomio 4x3
-5x2
+8x-5.
2.6. RESOLVER UNA ECUACIÓN.
Para resolver una ecuación en DERIVE, en primer lugar deberemos introducir la
expresión que define la ecuación “expresión1 = expresión 2”, y a continuación aplicar
la secuencia de menú Resolver-Algebraicamente (o bien aplicar el botón de
herramientas Resolver-Algebraicamente ) y aparecerá la siguiente ventana de
diálogo:
Si la ecuación tiene más de una variable, el programa nos solicita respecto de qué
variable queremos obtener la solución. Por ejemplo, si deseamos resolver la ecuación
x
2
-x-6=0, bastará que la introduzcamos en la ventana de álgebra, a continuación
aplicamos el botón Resolver Algebraicamente , hacemos clic sobre el icono
Simplificar y se obtiene
Prácticas de Matemáticas I y Matemáticas II con DERIVE 32
Hagamos un segundo ejemplo de una ecuación con más de una variable. Si
deseamos resolver la ecuación x
2
+y2
-8x+6y=169 respecto de la variable y; entonces
una vez editada con Edición Expresión la expresión anterior, aplicamos sobre ella
y elegimos la variable de resolución “y”, resultando
EJERCICIO 18.
Resolver las ecuaciones:
a) x2
-5x+6=0
b) 5(x-1/x2
)=x-1
c) x3
-1=0
d) Resolver respecto de la variable x la ecuación x+y2
-3xy=9
2.7. RESOLVER UNA INECUACIÓN CON MÁS DE UNA VARIABLE.
Para resolver una inecuación bastará editar la inecuación y aplicar sobre ella el
menú Resolver-Algebraicamente o el botón de herramientas . A continuación
elegimos la variable respecto de la cual deseamos resolver y luego hacemos clic en
SIMPLIFICAR.
Por ejemplo, si deseamos resolver la inecuación 3x-5y+7>0, primero la editamos
y en segundo lugar aplicamos , luego elegimos la variable respecto de la cual
resolver "x" y resulta
2.8. ASIGNACIÓN DE VALORES A VARIABLES, DEFINICIÓN DE
FUNCIONES Y SUSTITUCIÓN DE VARIABLES.
Es frecuente efectuar asignaciones de valores a variables. Este procedimiento se
ejecuta editando en DERIVE una expresión de la forma
“variable := valor”
Por ejemplo si deseamos asignar a la variable a, el valor 3, editamos la expresión
En adelante, cualquier expresión que contenga la variable a, siempre evaluara la
expresión tomando la variable a el valor asignado, en este caso 3. Así por ejemplo si
editamos la expresión “3ax+5” y la simplificamos, se obtiene
Operaciones algebraicas básicas 33
De igual forma que definimos variables, podemos DEFINIR FUNCIONES. Para
ello, seguiremos la siguiente sintaxis:
“nombre_función(var1,var2,...,varn) := expresión funcional”
Por ejemplo si deseamos definir la función mifuncion(x)=ln(x2
+2x-3), bastará que
editemos la expresión
Como puede observarse la función aparece escrita en mayúsculas. Esta es una
característica de DERIVE: todas las funciones definidas aparecen en mayúsculas en la
ventana de álgebra (aunque en la línea de edición se hayan escrito en minúsculas). Esta
definición es útil, ya que si deseamos evaluar esta función en x=5, bastará editar la
expresión “mifuncion(5)” y aplicar el comando Simplificar-Normal resulta
Si en una expresión dada deseamos sustituir el valor de una o varias variables sin
necesidad de asignar un valor a dichas variables, podemos utilizar el comando
Simplificar-Sustituir-Variables. Por ejemplo, si tenemos editada la expresión
y deseamos sustituir la variable “x” por el valor “5” y la variable “y” por el valor “30”
aplicaremos el comando Simplificar-Sustituir-Variables y aparece la ventana de
diálogo
en la que deberemos indicar para cada variable el valor de sustitución, marcando
primero la variable y luego tecleando el valor en el campo Sustitución:
Prácticas de Matemáticas I y Matemáticas II con DERIVE 34
al aplicar el botón se obtiene
si en vez de aplicar el botón hubiésemos aplicado el botón se
obtiene la simplificación de la expresión anterior, es decir
EJERCICIO 19.
a) Definir la variable “b” con el valor “34”.
c) Evaluar la expresión b+5.
d) Definir una función con el nombre mia(x,y)= x2
-3xy y evaluarla en x=2,y=4.
e) Editar la expresión
2 2
2( )
xy z
z xy
− +
+ +
y sustituir en ella la variable x por el valor
58 y la variable y por el valor 89, y obtener la expresión simplificada.
2.9. FUNCIONES PREDEFINIDAS EN DERIVE.
DERIVE tiene una colección de funciones predefinidas, es decir, funciones que no
necesitan de un fichero de utilidades para ser cargadas en memoria. Estas
funciones se encuentran por tanto, siempre disponibles. A continuación
mostramos algunas de estas funciones:
• Función raíz cuadrada: SQRT(x)
• Función valor absoluto: ABS(x)
• Función parte entera de x: FLOOR(x)
• Función resto de la división entera del número h entre m:
MOD(h,m)
• Función exponencial: EXP(x)
• Función logaritmo neperiano: LN(x)
• Función seno: SIN(x)
• Función coseno COS(x)
• Función máximo común divisor de los números a y b
GCD(a,b)
• Mínimo común múltiplo de los números a y b: LCM(a,b)
• Menor número primo mayor que el natural x:
NEXT_PRIME(x)
• Máximo común divisor de los polinomios a y b:
POLY_GCD(a,b)
• Factorial de n: n!
• Función media aritmética de argumentos dados:
AVERAGE(x1,x2,...,xn)
• Función varianza de los argumentos dados:
VAR(x1,x2,...,xn)
Operaciones algebraicas básicas 35
• Número de subconjuntos de p elementos de un conjunto m
(combinaciones) COMB(m,p)
• Módulo del complejo z: ABS(z)
• Argumento del número complejo z: PHASE(z)
• Parte real del complejo z: RE(z)
• Parte imaginaria del complejo z: IM(z)
• ....
La lista de funciones predefinidas se puede consultar en la
AYUDA de DERIVE.
2.10. LA AYUDA DE DERIVE.
Utilizando en el menú Ayuda podemos obtener ayuda de todos los comandos y
funciones definidas en DERIVE. En concreto podemos obtener varios tipos de ayuda.
Tenemos una ayuda en función de CONTENIDOS, de tal forma que al aplicar esta
opción se despliega una nueva ventana independiente del programa que tiene
agrupados por temas las ayudas que presta este programa:
El programa de ayuda tiene estructura de fichero hipertexto de tal forma que basta
ir pinchando las palabras subrayadas para acceder a la información que contiene el
programa de ayuda sobre ellas.
EJERCICIO 20.
Consultar en la AYUDA DE DERIVE la funciones predefinidas de DERIVE
Matematica
lunes, 11 de mayo de 2015
Teorema de pitagoras
Teorema de Pitágoras
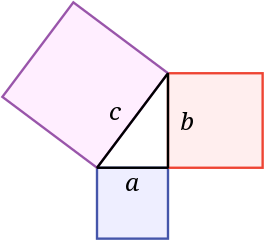
El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).
|
Si un triángulo rectángulo tiene catetos de longitudes  y
y 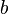 , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:
 y
y 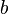 , y la medida de la hipotenusa es
, y la medida de la hipotenusa es  , se establece que:
, se establece que:(1)
| b | 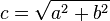 Historia[editar]
El teorema de Pitágoras tiene este nombre porque su descubrimiento recae sobre la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.
Designaciones convencionales[editar]
Demostraciones[editar]
El teorema de Pitágoras es de los que cuenta con un mayor número de demostraciones diferentes, utilizando métodos muy diversos. Una de las causas de esto es que en la Edad Media se exigía una nueva demostración del teorema para alcanzar el grado de "Magíster matheseos".
Algunos autores proponen hasta más de mil demostraciones. Otros autores, como el matemático estadounidense E. S. Loomis, catalogó 367 pruebas diferentes en su libro de 1927 The Pythagorean Proposition.
En ese mismo libro, Loomis clasificaría las demostraciones en cuatro grandes grupos: las algebraicas, donde se relacionan los lados y segmentos del triángulo;geométricas, en las que se realizan comparaciones de áreas; dinámicas a través de las propiedades de fuerza, masa; y las cuaterniónicas, mediante el uso de vectores.
China: el "Zhou Bi Suan Jing", y el "Jiu Zhang Suan Shu"[editar]
El "Zhou Bi" es una obra matemática de datación discutida en algunos lugares, aunque se acepta mayoritariamente que fue escrita entre el 500 y el 300 a. C. Se cree que Pitágoras no conoció esta obra. En cuanto al "Jiu Zhang" parece que es posterior, está fechado en torno al año 250 a. C.
El "Zhou Bi" demuestra el teorema construyendo un cuadrado de lado (a+b) que se parte en cuatro triángulos de base a y altura b, y un cuadrado de lado c.
Sea el triángulo rectángulo de catetos a y b e hipotenusa c. Se trata de demostrar que el área del cuadrado de lado c es igual a la suma de las áreas de los cuadrados de lado a y lado b. Es decir:
Si añadimos tres triángulos iguales al original dentro del cuadrado de lado c formando la figura mostrada en la imagen, obtenemos un cuadrado de menor tamaño. Se puede observar que el cuadrado resultante tiene efectivamente un lado de b - a. Luego, el área de este cuadrado menor puede expresarse de la siguiente manera:
Ya que
 . .
Es evidente que el área del cuadrado de lado c es la suma del área de los cuatro triángulos de altura a y base b que están dentro de él más el área del cuadrado menor:
Con lo cual queda demostrado el teorema.
Demostraciones supuestas de Pitágoras[editar]
Se estima que se demostró el teorema mediante semejanza de triángulos: sus lados homólogos son proporcionales.1
Sea el triángulo ABC, rectángulo en C. El segmento CH es la altura relativa a la hipotenusa, en la que determina los segmentos a’ y b’, proyecciones en ella de los catetos a y b, respectivamente.
Los triángulos rectángulos ABC, AHC y BHC tienen sus tres bases iguales: todos tienen dos bases en común, y los ángulos agudos son iguales bien por ser comunes, bien por tener sus lados perpendiculares. En consecuencia dichos triángulos son semejantes.
y dos triángulos son semejantes si hay dos o más ángulos congruentes.
Los resultados obtenidos son el teorema del cateto. Sumando:
Pero
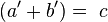 , por lo que finalmente resulta: , por lo que finalmente resulta:
Pitágoras también pudo haber demostrado el teorema basándose en la relación entre las superficies de figuras semejantes.
Los triángulos PQR y PST son semejantes, de manera que:
siendo r la razón de semejanza entre dichos triángulos. Si ahora buscamos la relación entre sus superficies:
obtenemos después de simplificar que:
pero siendo
 la razón de semejanza, está claro que: la razón de semejanza, está claro que:
Es decir, "la relación entre las superficies de dos figuras semejantes es igual al cuadrado de la razón de semejanza".
Aplicando ese principio a los triángulos rectángulos semejantes ACH y BCH tenemos que:
que de acuerdo con las propiedades de las proporciones da:
y por la semejanza entre los triángulos ACH y ABC resulta que:
pero según (I)
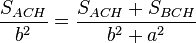 , así que: , así que:
y por lo tanto:
quedando demostrado el teorema de Pitágoras.
Es asimismo posible que Pitágoras hubiera obtenido una demostración gráfica del teorema.
Partiendo de la configuración inicial, con el triángulo rectángulo de lados a, b, c, y los cuadrados correspondientes a catetos e hipotenusa –izquierda-, se construyen dos cuadrados diferentes:
Si a cada uno de estos cuadrados les quitamos los triángulos, evidentemente el área del cuadrado gris (
 ) equivale a la de los cuadrados amarillo y azul ( ) equivale a la de los cuadrados amarillo y azul ( ), habiéndose demostrado el teorema de Pitágoras. ), habiéndose demostrado el teorema de Pitágoras.Demostración de Euclides: proposición I.47 de Los Elementos[editar] 
El descubrimiento de los números irracionales por Pitágoras y los Pitagóricos supuso un contratiempo muy serio.4 De pronto, las proporciones dejaron de tener validez universal, no siempre podían aplicarse. La demostración de Pitágoras de su teorema se basaba muy probablemente en proporciones, y una proporción es un número racional. ¿Sería realmente válida como demostración? Ante esto, Euclides elabora una demostración nueva que elude la posibilidad de encontrarse con números irracionales.
El eje de su demostración es la proposición I.475 de Los Elementos:
Basándose en la proposición I.412 de Los Elementos, que equivale a decir que a igual base y altura, el área del paralelogramo dobla a la del triángulo, (véase Figura Euclides 1).
Se tiene el triángulo ABC, rectángulo en C (véase Figura Euclides 3), y se construye los cuadrados correspondientes a catetos e hipotenusa. La altura CH se prolonga hasta J. Seguidamente se traza cuatro triángulos, iguales dos a dos:
Abundando en las anteriores consideraciones, nótese que un giro con centro en A, y sentido positivo, transforma ABD en ACK. Y un giro con centro en B, y sentido también positivo, transforma ABG en CBI. En lademostración de Leonardo da Vinci se encontrará nuevamente con giros que demuestran la igualdad de figuras.
Véase (en la Figura Euclides 3) que:
Pero siendo ACK=ABD, resulta que el rectángulo AHJK y el cuadrado ADEC tienen áreas equivalentes. Haciendosé razonamientos similares con los triángulos ABG y CBI, respecto al cuadrado BCFG y al rectángulo HBIJ respectivamente, se concluye que éstos últimos tienen asimismo áreas iguales. A partir de lo anterior, surge de inmediato que: "la suma de las áreas de los cuadrados construidos sobre los catetos, es igual al área del cuadrado construido sobre la hipotenusa".
Demostración de Pappus[editar]
Unos 625 años después que Euclides, Pappus6 parece seguir su senda, y desarrolla una demostración del teorema de Pitágoras basada en la proposicón I.363 de Los Elementos de Euclides:
Partimos del triángulo ABC rectángulo en C, sobre cuyos catetos e hipotenusa hemos construido los cuadrados correspondientes.
Prolongando CH hacia arriba se obtiene el rectángulo CEGI cuya diagonal CG determina en aquél dos triángulos rectángulos iguales al triángulo ABC dado:
En consecuencia los triángulos rectángulos ABC, ICG y EGC tienen sus tres lados iguales.
De 1) y 2) se sigue que las superficies de ACED y AHMN son iguales.
Análogamente:
De dónde se deduce la equivalencia de las superficies de BLMH y de CIKB.
El teorema de Pitágoras queda demostrado.
Demostración de Bhaskara[editar]
Bhaskara II, el matemático y astrónomo hindú del siglo XII, dio la siguiente demostración del teorema de Pitágoras.
Con cuatro triángulos rectángulos de lados a, b y c se construye el cuadrado de lado c –izquierda-, en cuyo centro se forma otro cuadrado de lado (a-b).
Redistribuyendo los cuatro triángulos y el cuadrado de lado (a-b), construimos la figura de la derecha, cuya superficie resulta ser la suma de la de dos cuadrados: uno de lado a –azul- y otro de lado b -naranja-.
Se ha demostrado gráficamente que

Algebraicamente: el área del cuadrado de lado c es la correspondiente a los cuatro triángulos, más el área del cuadrado central de lado (a-b), es decir:
expresión que desarrollada y simplificada nos da el resultado
 , y el teorema queda demostrado. , y el teorema queda demostrado.Demostración de Leonardo da Vinci[editar]
En el elenco de inteligencias que abordaron el teorema de Pitágoras no falta el genio del Renacimiento,Leonardo da Vinci.
Partiendo del triángulo rectángulo ABC con los cuadrados de catetos e hipotenusa, Leonardo añade los triángulos ECF y HIJ, iguales al dado, resultando dos polígonos, cuyas superficies va a demostrar que son equivalentes:
Comparemos los polígonos destacados en gris, ADGB y CIJA:
Se concluye que ADGB y CIJA son iguales.
De modo análogo se comprueba la igualdad entre ADGB y CBHI.
Además, de un modo semejante a lo explicado en la demostración de Euclides, nótese que un giro de centro A, y sentido positivo, transforma CIJA en ADGB. Mientras que un giro de centro B, y sentido negativo, transforma CBHI en ADGB.
Todo ello nos lleva a que los polígonos ADEFGB y ACBHIJ tienen áreas equivalentes. Pues bien, si a cada uno le quitamos sus dos triángulos –iguales- las superficies que restan forzosamente serán iguales. Y esas superficies no son sino los dos cuadrados de los catetos en el polígono ADEFGB, por una parte, y el cuadrado de la hipotenusa en el polígono ACBHIJ, por la otra. El teorema de Pitágoras queda demostrado.
Demostración de Garfield[editar]
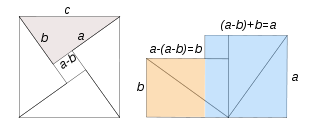
James Abram Garfield (1831-1881), el vigésimo Presidente de los Estados Unidos,7 desarrolló una demostración del teorema de Pitágoras publicada en el New England Journal of Education.
Garfield construye un trapecio de bases a y b, y altura (a+b), a partir del triángulo rectángulo de lados a, b y c. Dicho trapecio resulta compuesto por tres triángulos rectángulos: dos iguales al dado, y un tercero, isósceles de catetos c. En consecuencia:
como corresponde a la superficie del trapecio, pero asimismo tenemos una figura compuesta por tres triángulos, dos de ellos iguales, de modo que:
multiplicando ambos lados por
 y simplificando... y simplificando...
expandiendo el miembro derecho...
restando
 a ambos miembros, finalmente nos da: a ambos miembros, finalmente nos da:y el teorema está demostrado. |
Suscribirse a:
Entradas (Atom)
















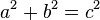
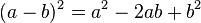
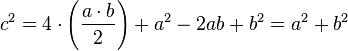

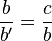


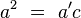
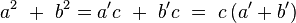


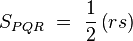
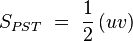
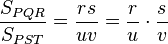
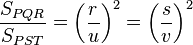
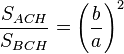
 (I)
(I)